月度归档： 2024 年 6 月

常言道，温故而知新。我们总是借助熟悉的事物，已经搞明白的事物作为支架来理解陌生的事物。这应该成为教育的法则，所谓最近发展区，可以类比为人们内在的已经成熟的结构。
生态的类比，所有的生长，都是不断的在原有的基础上进行建构，不断丰富分化形成新的系统和结构。学习就是这样的一个过程。不知道从什么时候开始，建构这个名词冒了出来，很时髦，就好像知识跟盖房子一讲堆到那里，绑上钢筋就OK了。这怎么可能。
我们继续改变的就是对教育和学习的机械的不合时宜的类比。学习想生长一样，而不是建筑，不是装修。那种没有生命力的知识体系，可以作为装点门面的花瓶，但是不能进行创新和创造。还侵占了原有的生态空间。构巢而居，无可厚非。但是没有边界，贪得无厌，恨不得把所有的土地都堆成高楼就不合时宜了。
所谓最近发展区，不是空房子，而应该是含苞待放的花蕾，是枝枝叉叉附近的芽。这才是比较合适的类比

平衡是物体或者结构的一种普遍的状态，利用平衡我们可以分析各部分之间的力学关系。随着计算机的发展，各种结构仿真程序已经能够实现有限元的结构分析，可以在产品没有上线之前，就能较为准确的发现产品结构的可靠性、设计的合理性、安全性等内容，以避免研发阶段人力物力等资源的巨大浪费。而这项技术的源头就是我们所学习的受力分析的内容。下面我们就来纵览这一技术的发展历程。
一、对称性和二力平衡
新物理学诞生以来，人类渐渐搞清楚了力和运动的关系，发现力并不是维持物体运动的原因，而是改变物体运动的原因。处于静止或者匀速直线运动的物体，并不需要外力来维持。而当物体的受力平衡的时候，也相当于物体不受外力，处于平衡态。
最简单莫过于二力平衡，二力平衡的依据是数学的和哲学的。当两个力等大反向的时候，物体没有不平衡的理由，所以平衡。这有点不讲理，但是很可靠，也是整个力学分析大厦的基础之一。
二力平衡是一维的平衡，在涉及一维的多力平衡的时候，我们可以用代数方法顺利解决，包括一维的动态平衡和临界问题。
二、实验定律
随着实践的丰富和研究对象所处环境的复杂程度提高，我们有必要将二力平衡的技术拓展到二维甚至是三维，从单体平衡的技术拓展到多体平衡，从静态平衡到动态平衡等等。这一切新的实践挑战，迫切需要我们创建新的理论，开发新的技术。
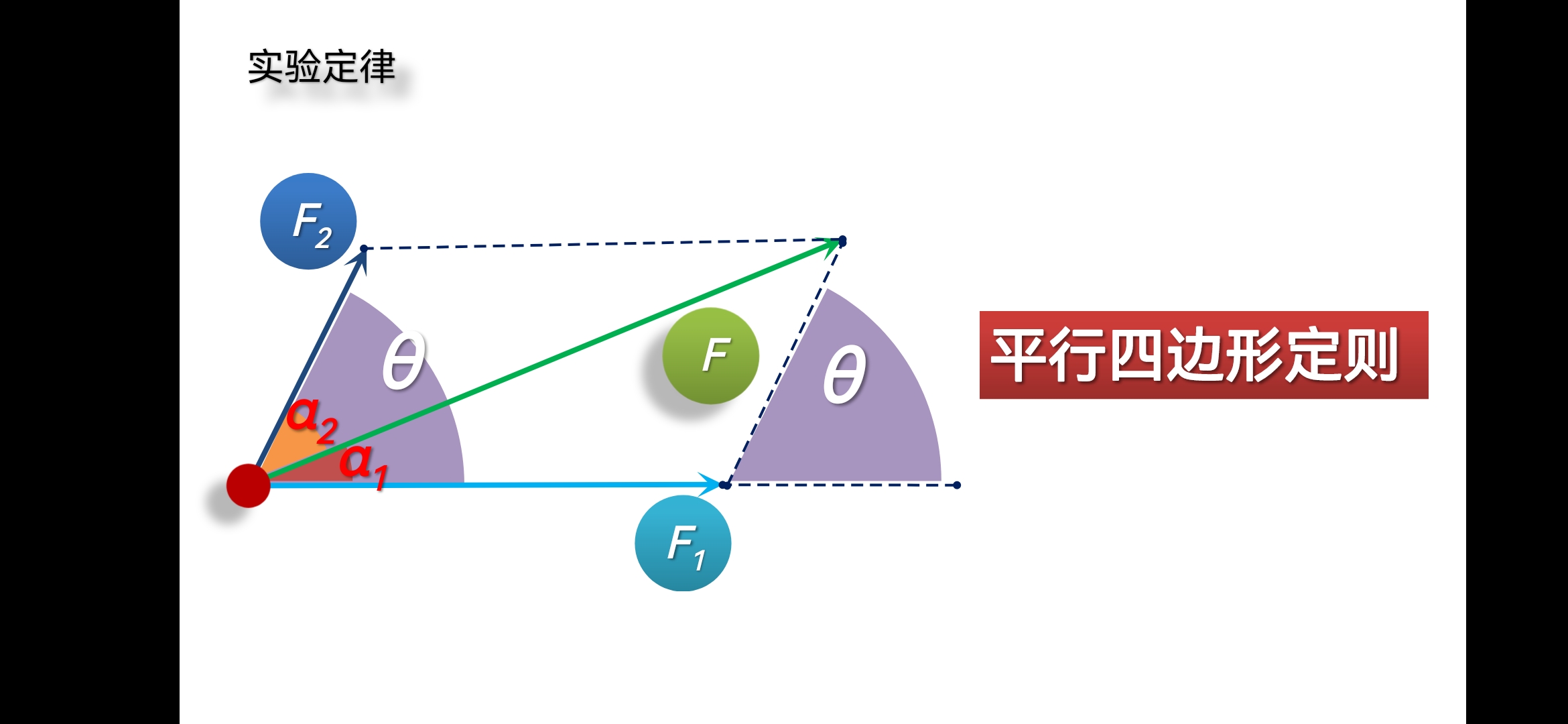
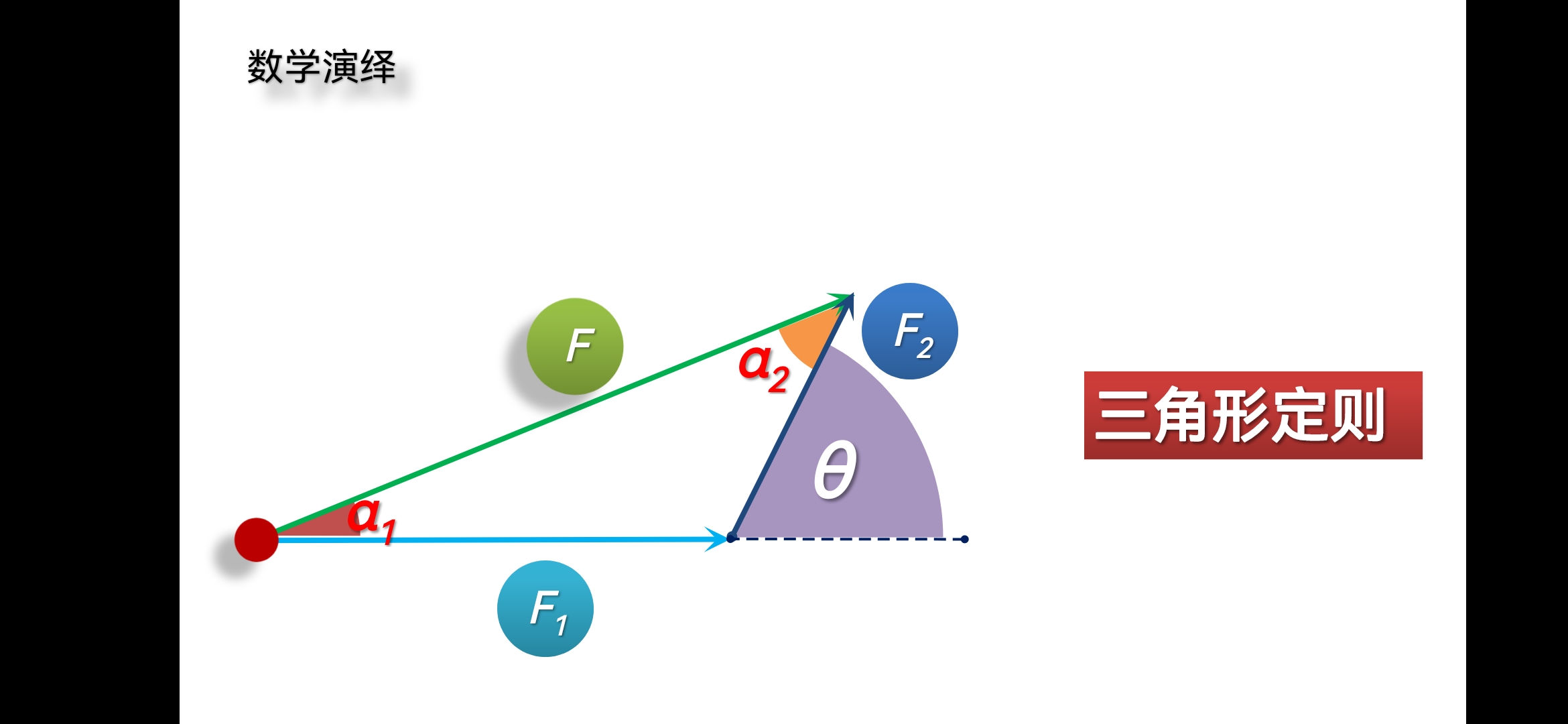
物理从本质上看就是观物取象，格物致知。力的平衡的研究是从观察开始的，但更深入的研究一定需要格物致知。我们就让物体实际的处于三力平衡的状态，然后直接去测量物体所受到的三个力，并用图示表现出来。通过绘图我们会发现，当三力平衡的时候，其中两个力的合力，从效果上看相当于是一个以表示这两个力的有向线段为邻边的平行四边形的对角线代表的力。这就是平行四边形定则的内容，也是力的平衡领域的一个重要的实验定律。
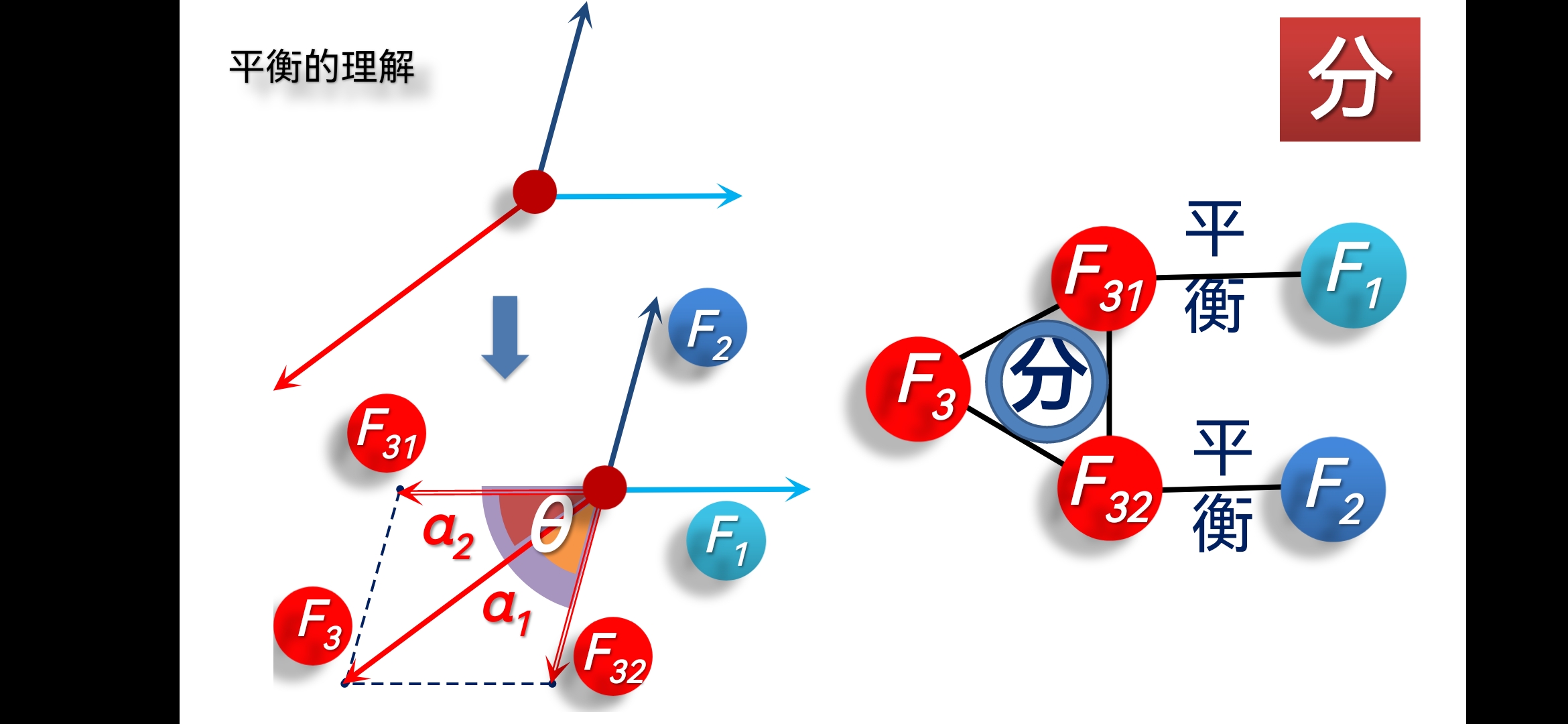
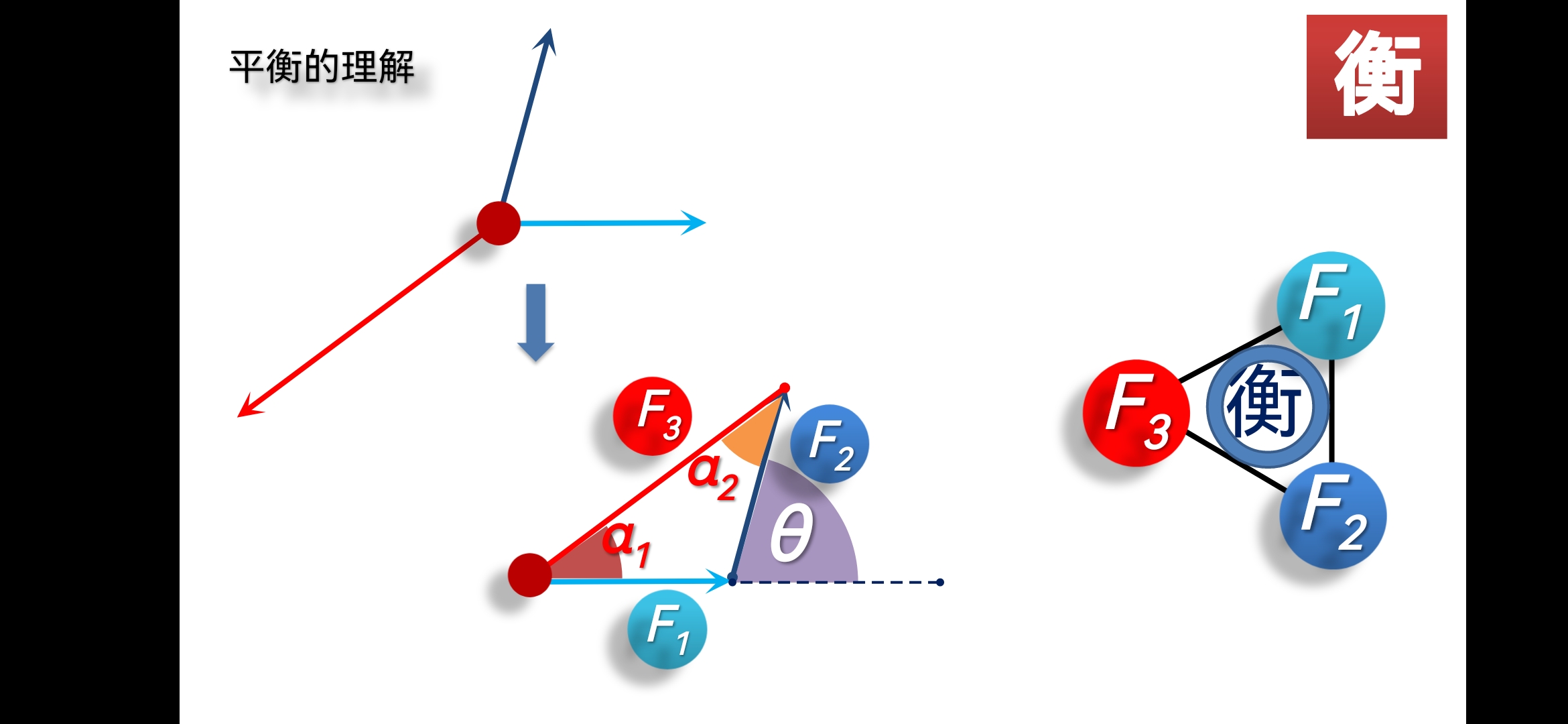
为了表述平行四边形定则，我们建立了分力和合力的概念，明确了合力和分力之间的数学关系，也就获得了理解其他复杂平衡的方法。这一方法的核心思想就是：降维。三力平衡可以用合成法转化为其中二力的合力与第三个力的一维的二力平衡问题；或者用分解法转化为其中一个力的合力的两个分力与另外两个力分别一维二力平衡的问题；或者是用正交分解法转化为选定方向上的一维的多力平衡问题。这些都是可以用代数方法直接列式和计算的。
至此，以结点（物体）为联系的纽带、以平衡为规则，我们就掌握了对任何复杂结构的进行分析的本领。
三、五大关系
物体所处的环境是复杂多样的，结构形式也是复杂多样的。为了顺利完成受力分析的任务，我们还需要探索和储备一些关系才行。具体可以称为五大关系：等效关系、平衡关系、失衡关系、对称关系和切法关系。
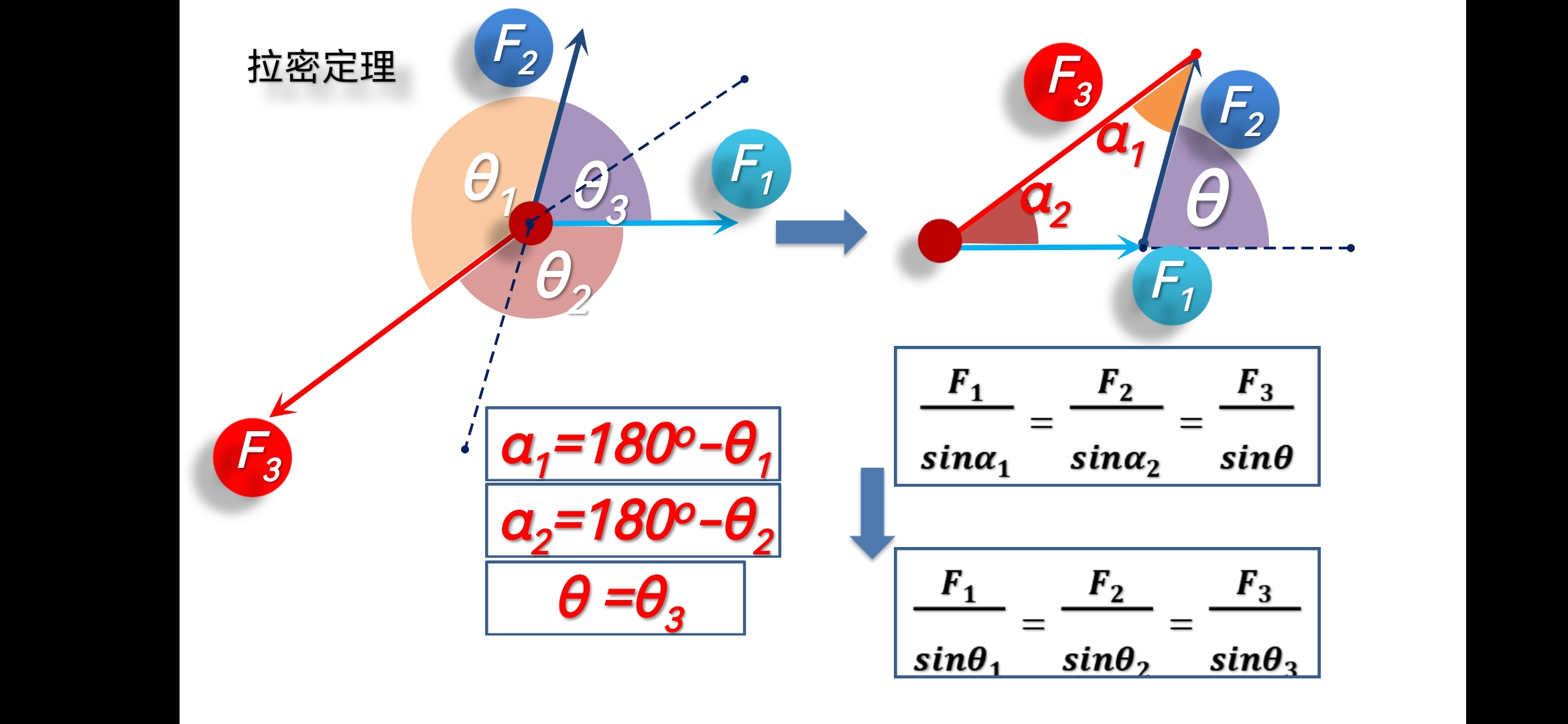
等效关系：是指合力和分力的关系。在构建平行四边形、三角形或者多边形之后，我们可以通过几何规律（如勾股定理、余弦定理、正弦定理、拉密定理、相似三角圆的性质等等）获得各力之间的数量关系。
平衡关系： 平衡意味着物体处于平衡态时，各方向或人为选定的方向上必须满足合力为零。
失衡关系：表现为a和F之间的因果联系，a之于F如影之随形。当物体在某个方向有加速度（ax，ay，an）时，在该方向必有合力不为零，且F合=ma。
对称关系：表现为相互作用，两物体之间发生相互作用时，彼此作用力一定等大反向。
切法关系：这是一个实验定律，或者更确切的说是一个物理模型（库伦平面）。这个库伦就是电学中发现库仑定律的那位大神。对于这种平面，我们可以提供两个信息：一个是摩擦系数，表达了接触面法向力和切向力-滑动摩擦力之间的关系；一个是最大静摩擦力，表达了接触面抗拒侧向扰动的能力上限。
如上所述，只要我们想去寻找某两个力之间的关系的时候，一定需要从上述五个关系中进行挑选。这是编制力学关系网的经纬。
（题外话：五大关系给出的仅仅是关系，但是如果想知道系统或者结构中各个力的具体数值，还应该有一个入口或者说锚点，常见的就是重力，弹簧弹力和各种场力；亦或是力的作用效果a，ΔE/Δx, Δp/Δt）
四、结构分析的视觉线索
经过之前的论述，我们已经完成了情境感知、模型建构的工作。下面进入问题解决和策略成熟阶段。要学会分析各种结构的合理性、稳定性和可靠性。
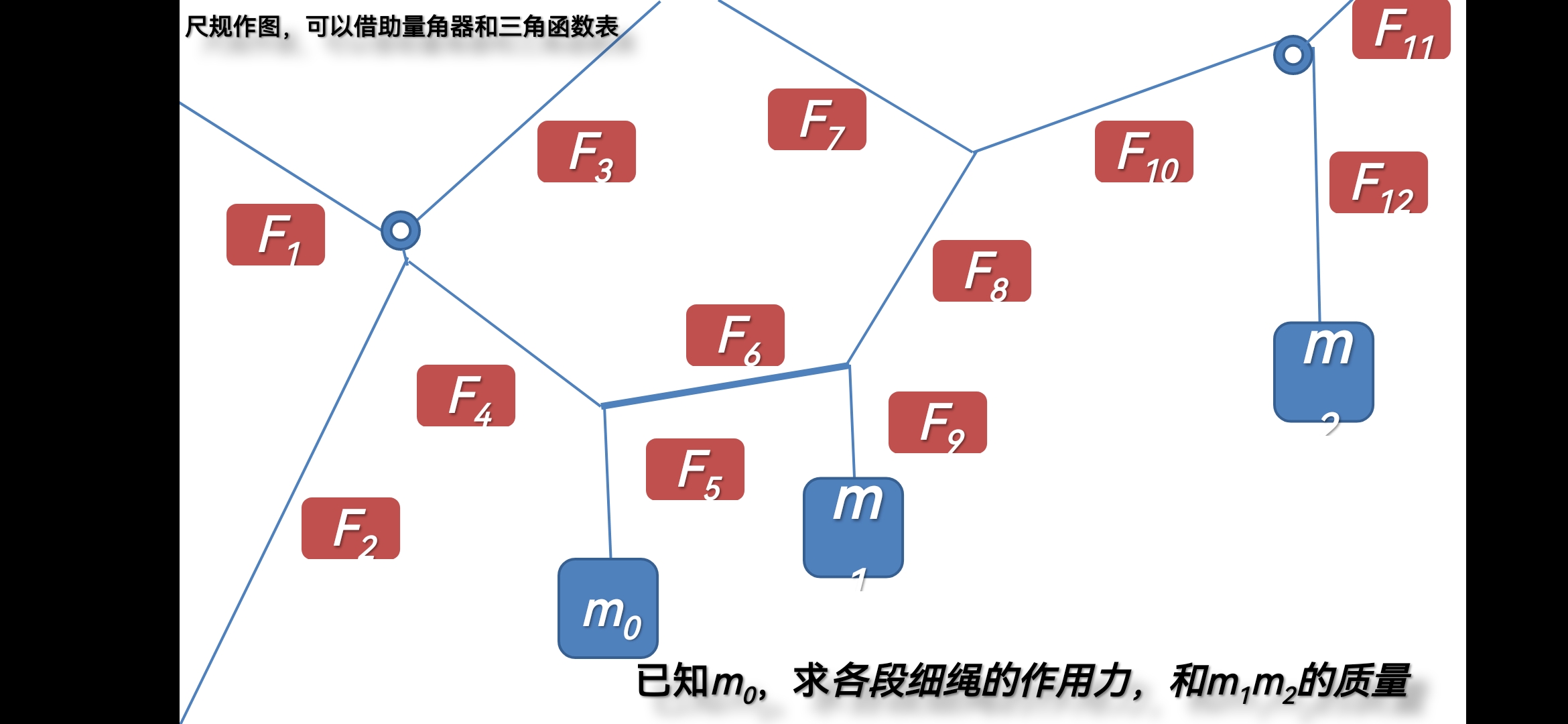
结构可笼统的分类为张拉结构、框架结构和堆叠拼插结构。张拉结构关心的是结点和结点（活结和死结）所联系的各绳上的作用力；框架结构关注的是支架中杆（活杆和死杆）的受力；堆叠拼插结构关心的是接触面上的弹力和切向的摩擦力。结构分析就需要我们能够用画面中提供的视觉线索，来搞定各部分的受力情况。
所谓视觉线索就是物体的结构（θ），物体的形变（x）和物体的变速（a）等。“会看的看门道”就是在说这个意思。那么你能够通过结构图直接看到力的关系吗？如何修炼这种洞察力呢？
倾斜和水平绳悬挂物体中，θ就是力学分析的视觉线索，不同的θ值，就意味着，三个共点力之间大小关系。可以用三角函数，或者拉密定理来表达。这样以重力为一点我们就可以完成整个网络的受力分析。（所以观察问题的角度真的很重要）
含弹簧的悬挂结构中，（θ和x）就是力学分析的视觉线索，从x和k我们可以直接得到弹簧上的弹力。然后利用五大关系推演其他作用力。
*处于变速运动中的组合体，（a）就是力学分析的视觉线索，可以用a，ΔE/Δx, Δp/Δt确定合力的大小，然后再根据五大关系推演其他作用力。
综上所述，我们就非常笼统地走完了力学分析的全部历程。以此为主干，再进行局部的丰富和精装修，从而构建自己受力分析的案例库、技能群和工具包。“路漫漫其修远兮，吾将上下而求索。”要坚信事物是复杂的，但在一段时间内又是稳定的不变的。我们可以通过有顺序有章法的探索，获得对事物的理解和驾驭。
这些思考并不能在书本学习阶段获得，反而是离开书本后，真的进行技术实践时才能得到的感悟。科学、技术是不分家的，没有科学理论的传承发展，技术就成了无本之木，无源之水。若没有技术的开发利用，科学的花园也不会百花齐放姹紫嫣红。

探索者
每一个健康正常的系统，都会自然的出现叛逆者。秩序的尽头是混乱。混乱的尽头是秩序。自古皆然。所谓分久必合,合久必分。
完形是暂态，碎片化才是常态。人的一生就是对抗碎片化的过程，所谓新陈代谢，就是吐故纳新。我们必须不断摄入有秩序的，低熵的东西，才能对抗生命的流逝。越是秩序，生命力就越是旺盛。越是用心，事业就越是顺遂。秩序和混乱就是这样的一对矛盾，能够在一片噪音中保持定力的本事是个人成就的关键能力。
大部分的系统，对待先行者都不甚友好。原因在于，革命者和改革者的特点就是破旧立新，推陈出新。他们工作的出发点就是否定现实，然而没有任何人喜欢被否定。这种自恋是与生俱来的。于是，探路者的命运时常是，坠而亡者半，饥而亡者半，路遂绝。
一个系统的成熟，不在于装点了多少碎片。而在于对变革有多么宽容。那是未来的种子，而不是不务正业的逆子。

碎片化教学何时休
​ -物理学教法实验室
分析是把事物分解为各个部分、侧面、属性，分别加以研究。是认识事物整体的必要阶段。综合是把事物各个部分、侧面、属性按内在联系有机地统一为整体，以掌握事物的本质和规律。
分析与综合是互相渗透和转化的，在分析基础上综合，在综合指导下分析。分析与综合，循环往复，推动认识的深化和发展。一切论断都是分析与综合的结果。
​ 当前，基础教育界已经成为概念碎片化的重灾区。概念名词一箩筐，各种理论汗牛充犊。大小论文，滔滔不绝，连绵不绝，根本停不下来。然而这种“繁荣”的背后，并不是教科研生态的欣欣向荣，反而是教科研生态衰败的表征。大家都陷入了概念名词的高强度空转之中，却不挂任何负载，不解决具体问题，纯粹一个自圆其说，自得其乐。说的天花乱坠，骨子里还是个应试教育，还是一个资源决定论。人的主观能动性，被大大的低估了。
​ 功利之心容不下家国情怀。
​ 功利之心的特点就是，投机钻营，见好就上有利就上。真相对其毫无约束力，道德更是手下败将。大家都演的天衣无缝，何必掀桌子呢。
​ 然而，我们的代价是高昂的，社会的代价是高昂的。我们用看似严整，实则严重碎片化的材料，充当了教育的主要或者说全部内容，在实施方面更是把时间和精力的碎片化发挥到了极致名义上是利用碎片时间，其实是在认为的进行切割。一定不让学生有长时间的思考，反思，一定要搞的他们，疲于奔命，不求甚解，囫囵吐枣，邯郸学步，人云亦云。
​ 没有什么整体设计，顶层设计。没有情景整合，没有高阶问题，没有历史和逻辑的线索，就是一个题海，包打天下，一个经验主义包打天下。好就全好，爱屋及乌，差就全差，恨屋及乌。蓝图天天换，路线天天变，方向兜兜转，目标隐又现。这不是危言耸听，这是普遍的事实。
​ 时至今日，我们已经有了足够的理由，能力和资源来创造一个更为和谐的教学环境，学习模式。然而思维的惯性却组织我们，做出哪怕一点常识。
​不喜欢变化，只喜欢守正，不喜欢创新。
​ 然而当一个系统，出现了全局性的，结构性的问题的时候，局部的小打小闹已经无济于事了，改良主义，现在已经不合时宜。
​唯有突破性的变革才能成功。